A survey in seven questions.
Q 1. What do we use geometric morphometrics for?
A 1. We need geometric morphometrics for answering questions about how parts of a body vary or how they respond to processes like growth, evolution, or injury, or about how we control these parts of a body (like by nutrition or surgery or animal husbandry) or how we react to parts of a body (like by calling a face beautiful or sexy). All these processes can be understood or the questions answered by talking about how points are "pushed around," and geometric morphometrics is the best way to talk about the patterns for what the points are doing during all these processes - and about the exceptions to these patterns, like birth defects. Geometric morphometrics combines rich data sets from modern medical imaging devices looking at organisms with strict rules for how to talk about the differences in the size and shape of the organisms being studied. It is very useful in every single branch of anthropology, and also in many other fields like cognitive psychology and medicine.
To talk about geometric morphometrics we need to introduce three other words first - see the next two questions.
Q 2. What is morphometrics?
A 2. Morphometrics is a collection of tools for treating information about the geometry of organisms by statistical methods - talking about their variation and the uncertainty of conclusions we draw about them.
Q 3. Oh, yes. What is statistics? what is geometry?
A 3. Statistics consists of methods for learning from measurements under conditions of uncertainty (this can mean uncertainty about measurements or uncertainty about the theories that are supposed to explain the measurements).
Geometry is what you studied in Gymnasium or in high school: the rules for making sense of data about positions, distances, and angles in our ordinary three-dimensional world. You remember that some of geometry is about ways of measuring distances or angles, while another part of geometry is about the "theorems" that tell you how the measures have to come out sometimes.
Q 4. OK, now what is geometric morphometrics?
A 4. GEOMETRIC MORPHOMETRICS is the statistical analysis of a particular
kind of geometric information about organisms: information about exactly where the parts of the organism are with respect to each other. Geometric morphometric tools combine morphometrics (geometry of organisms), computer science, and modern engineering to focus on information from the actual locations of points on or inside organisms. We need the engineering to get this information from complicated three-dimensional objects like fossils or faces, and we need computer science to process the huge amount of information that we get from a the surface or the inside of more than one whole organism.
Q 5. What information does geometric morphometrics use?
A 5. In geometric morphometrics, information comes from mathematical points (the tiniest possible locations) taken a few at a time or else many at a time. The simplest kind of data is from just a list of points, like "the tip of the nose and the center of the earhole and the center of the forehead." More complicated data can come from the outer surface of a form, an internal boundary surface between two of its parts, or a curve (like a nerve fiber) that wanders inside the organism, and this more complicated information can be studied by the same methods that work for the lists of points.
Q 6. What is so special about geometric morphometrics?
A 6. There is a mathematical problem here that is much more difficult than you might think - its solution was worked out only about 30 years ago: how to talk about the locations of all these points and parts in a way that doesn't lead to arguments. One trick is not to talk about position, actually, but only about the distances between different positions of the same landmark point.
There is also a second trick: to study the shape of a form and its size separately, and combine them only at the end. When we average a set of forms, for instance, or explain them by age or genes, we are actually averaging their size and their shape separately, or predicting (explaining) their size and shape separately. At the end, we go back to computer science for another important tool, the display of shape differences as deformations. These animated graphics use a surprising range of your own visual abilities to turn the statistical findings back into patterns you can understand on the computer screen or in the virtual space of a 3D display right in front of you.
Q 7. What are some other words I will run into?
A 7. Here are some more important terms in geometric morphometrics:
landmarks - the named points, curves, or surfaces whose locations are tracked
Procrustes coordinates - numbers for the shape of a sample of sets of landmarks
Thin-plate spline - a formula for turning the movement of a set of landmarks into a graphic that looks like a deformation
Shape regression - a statistical method for finding how a shape depends on factors that predict it (evolution) or that it predicts (attractiveness)
Allometry - the dependence of shape on size (not specific to geometric morphometrics, but across all of biology)
Now go back and read the answer to question 1 again.
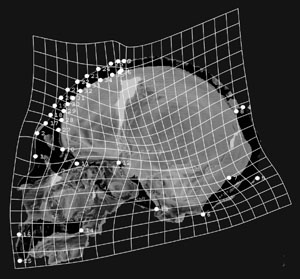
Thin plate spline
An interpolation algorithm, the so called "thin plate spline" (TPS), was borrowed from material physics and was introduced to morphometrics by Fred Bookstein. It generates a deformation grid between two point configurations ...
Procrustes superimposition
Shape variables are usually constructed by a Procrustes superimposition. The raw coordinates are superimposed by translating the configurations to a common centroid, scaling to unit centroid size, and rotating until the sum of the squared distances ...
Semilandmarks
A recent extension of the Procrustes superimposition is the sliding landmark algorithm. Traditional landmarks need to be identifiable in all two or three dimensions of physical space in order to precisely locate them on every specimen.