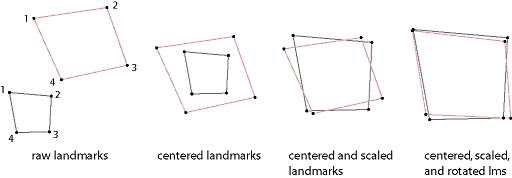
Shape variables are usually constructed by a Procrustes superimposition. The raw coordinates are superimposed by translating the configurations to a common centroid, scaling to unit centroid size, and rotating until the sum of the squared distances between corresponding landmarks is minimized. The remaining Procrustes coordinates describe shape per se.

Among the linear multivariate statistical methods applied to Procrustes coordinates of landmarks and semilandmarks, perhaps the most useful is Principal Component Analysis (PCA), which , as in any other application, is used mainly to reduce the number of variables and to simplify explanations. Because of how easy it is to sample many landmarks with modern digitizers, there are a lot of shape coordinates in most applied studies. PCA, which is called relative warp analysis when applied to shape coordinates, provides the low dimensional summary that we need.

A particular advantage of geometric morphometrics is that multivariate statistical results like PCA can be visualized as shapes or shape changes. Similarly, multivariate regressions of Procrustes shape coordinates on some external variable (such as centroid size, behavioural or ecological variables) - which is called shape regression - can be visualized as shape deformation. Another very useful tool is Partial Least Squares (PLS) analysis (called singular warp analysis in geometric morphometrics) allowing one to assess the pattern of covariation between two or more blocks of variables.

A recent addition to the morphometric synthesis is PCA of size-shape space. The augmentation of the shape variables by the logarithm of centroid size allows one to study patterns of size and shape (i.e. form) together. This has turned out to be of particular importance for developmental studies or discrimination studies.